Т.к. АВ=3NB, то AN=2NB, следовательно AN в два раза больше NB, а значит углы напроив этих сторон отличаются в два раза и следовательно угол BKN в два раза меньше угла NKA (который 90 град), получаем, что угол NKB равен 45 град.
Тогда угол AKC 180-90-45 = 45 град.
Тогда угол KAC 180-90-45 = 45 град. Значит треугольник АКС прямоугольный равнобедренный и АС=СК и так как АК биссектриса, то СК=ВК и = АС.
По условиям угол АДВ=углу СДА, а так как диагональ в трапеции является секущей при её параллельных основаниях, то угол СВД=углу АДВ, как внутренние разносторонние, и следовательно равен углу СДВ. Рассмотрим ∆ВСД. Так как 2 угла при его основании равны, то он является равнобедренным и стороны ВС=СД=10см. Проведём высоту СН. Она делит нижнее основание так, что АН= ВС=10см, тогда отрезок НД=18-10=8см. Рассмотрим ∆СДН. Он прямоугольный так как Н - высота. Также в нём уже известны 2 стороны, и теперь можно найти высоту СН по теореме Пифагора: СН²=СД²-НД²:
СН=√(10²-8²)=√(100-64)=√36=6см;
СН=6см. Теперь найдём площадь трапеции зная высоту по формуле:
Объяснение:
Не уверен, но вариант такой:
Т.к. АВ=3NB, то AN=2NB, следовательно AN в два раза больше NB, а значит углы напроив этих сторон отличаются в два раза и следовательно угол BKN в два раза меньше угла NKA (который 90 град), получаем, что угол NKB равен 45 град.
Тогда угол AKC 180-90-45 = 45 град.
Тогда угол KAC 180-90-45 = 45 град. Значит треугольник АКС прямоугольный равнобедренный и АС=СК и так как АК биссектриса, то СК=ВК и = АС.
Для прямоугольного треугольника АКС получаем
квадрат АК= квадрату АС + квадрат КС
квадрат АК = квадрат ВК + квадрат ВК
АК = ВК х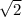
ответ: S=84см²
Объяснение:
По условиям угол АДВ=углу СДА, а так как диагональ в трапеции является секущей при её параллельных основаниях, то угол СВД=углу АДВ, как внутренние разносторонние, и следовательно равен углу СДВ. Рассмотрим ∆ВСД. Так как 2 угла при его основании равны, то он является равнобедренным и стороны ВС=СД=10см. Проведём высоту СН. Она делит нижнее основание так, что АН= ВС=10см, тогда отрезок НД=18-10=8см. Рассмотрим ∆СДН. Он прямоугольный так как Н - высота. Также в нём уже известны 2 стороны, и теперь можно найти высоту СН по теореме Пифагора: СН²=СД²-НД²:
СН=√(10²-8²)=√(100-64)=√36=6см;
СН=6см. Теперь найдём площадь трапеции зная высоту по формуле:
S=(ВС+АД)÷2×СН=(10+18)÷2×6=28÷2×6=
=14×6=84см²; S=84см²