2. В основании пирамиды лежит равнобедренная трапеция с углом 30°. Каждая боковые грани наклонены к основанию под углом 60°. Высота пирамиды равна 3√3. Найдите объем пирамиды.

Дано:

ΔABC, ∠B = 90°.

Вписанная окружность с центром O и радиусом OD = OE = OF,

D∈BC, E∈AC, F∈AB.

OE = 12 (см), EC = 8 (см).

Найти:

Заметим, что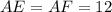  и   (так как отрезки касательных, проведенных к окружности из одной точки, равны).

Пусть .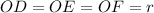

Тогда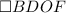 - квадрат, так как 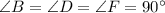(и, значит, 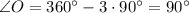), а также 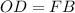, 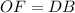и 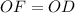. - Все стороны и углы данного четырехугольника равны.

Значит, .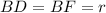

Тогда катеты треугольника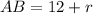 и 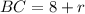, а гипотенуза равна .

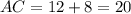По тереме Пифагора:

Второй корень нам не подходит (он отрицательный ... ).

Так что .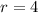

Можем найти площадь:

Задача решена!

96  см².

Обозначим данные прямые через l0 и l, данные точки на прямой l0 - через A0, B0, C0, данные точки на прямой l - через A, B, C. Пусть l1 - произвольная прямая, не проходящая через точку A. Возьмем произвольную точку O0, не лежащую на прямых l0 и l1. Обозначим через P0 центральное проектирование прямой l0 на прямую l1 с центром в точке O0, а через A1, B1, C1 - проекции точек A0, B0, C0. Пусть l2 - произвольная прямая, проходящая через точку A, не совпадающая с прямой l и не проходящая через A1. Возьмем некоторую точку O1 на прямой AA1 и рассмотрим центральное проектирование P1 прямой l1 на l2 с центром в O1. Обозначим через A2, B2, C2 проекции точек A1, B1, C1. Ясно, что A2 совпадает с A. Наконец, пусть P2 - проектирование прямой l2 на прямую l, которое в том случае, когда прямые BB2 и CC2 не параллельны, является центральным проектированием с центром в точке пересечения этих прямых, а в том случае, когда прямые BB2 и CC2 параллельны, является параллельным проектированием вдоль одной из этих прямых. Композиция P2°P1°P0 является требуемым проективным преобразованием.

Объяснение:

пример