Через кінець А відрізка АВ проведено площину Через Bi точку (відріз ка AB проведено паралельні прямі, які перетинають площину ауточках Віі Ci. Обчислити ВВі. Якщо CC = 16см, AC/AB =4/5
Розв'язання: Проведемо медіану до основи BC у точку K, тоді CK = BK =
= BC : 2 = 10 : 2 = 5 см.Нехай медіани AK і BM - перетинаються в
точці O.За теоремою про медіану, медіани точкою перетину діляться у відношенні 2 : 1, рахуючи від вершини кута.Введемо коефіціент пропорційності y, тоді BO = 2y,MO = y, так як медіани AK і BM - перетинаються в точці O.
BM = BO + MO;
8 = 2y + y;
8 = 3y;
y = ;
BO = 2y = 2 * ; MO = y = ;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора: ;
Введемо коефіціент пропорційності x, тоді OK = x, AO = 2x за теоремою про медіану, так як медіани AK і BM - перетинаються в точці O.
AK = OK + AO;
AK = x + 2x = 3x = 3*OK = ;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора:
ответ:1) так как треугольник АBC равно едренный => BD- медиана, высота, биссектриса=> угол ADB=90 градусов;
Так как BD- биссектриса=>угол ABD= углу DBС= угол ABC/2=78/2=39 градусов
ответ:90;39
2)так как D-середина AB=>BD=AD; так как Е-середина ВС=>СЕ=ВЕ; так как AD=EC=>BD=AD=CE=BE и AB=BC;
Треуголники АВЕ и СDB равны по двум сторонам и углу сежду ними(DB=BE; AB=BC; угол В- общий) Ч. Т. Д.
3)треугольники ОАВ и СОD равны по двум углам и ребру между ними ( OA=OC- по условию; угол А=углу С- по условию; угол О- общий) Ч. Т. Д.;
Так как треуголники равны=> у них все ребра тоже равны=> АВ=DC=15см
ответ: 15см
Объяснение:
AB = AC =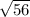
см
Объяснение:
Дано:
AC = AB, BC = 10 см, BM = 8 см, CM = MA
Знайти: AC,AB - ?
Розв'язання: Проведемо медіану до основи BC у точку K, тоді CK = BK =
= BC : 2 = 10 : 2 = 5 см.Нехай медіани AK і BM - перетинаються в
точці O.За теоремою про медіану, медіани точкою перетину діляться у відношенні 2 : 1, рахуючи від вершини кута.Введемо коефіціент пропорційності y, тоді BO = 2y,MO = y, так як медіани AK і BM - перетинаються в точці O.
BM = BO + MO;
8 = 2y + y;
8 = 3y;
y =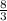
;
BO = 2y = 2 *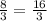
; MO = y = 
;
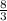За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора: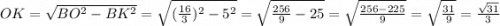
;
Введемо коефіціент пропорційності x, тоді OK = x, AO = 2x за теоремою про медіану, так як медіани AK і BM - перетинаються в точці O.
AK = OK + AO;
AK = x + 2x = 3x = 3*OK =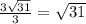
;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора:
Так як AB = BC за умовою, то AB = AC =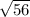
см.