Даны точки А(25;-9;13) и В(8;14;2). Найдите расстояние от точки А до плоскости OXY.
2. Найдите скалярное произведение векторов {-4;7;1} и {5;5;1}.
3. Даны точки А(-5;2;0), В(-4;3;0), С(-5;2;-2).Найдите длину средней линии треугольника АВС, соединяющей его меньший катет и гтпотенузу.
4. Определите вид четырехугольника АВСD, если А(6;7;8), В(8;2;6),С(4;3;2),D(2;8;4).

Показать ответ

Ответ:

aliskaiii

11.03.2020 19:26

1) Экскурс в теорию: угол между плоскостями (ВАС) и (САН)- двугранный угол (НАСВ) измеряется градусной мерой линейного угла L HCB , образованного лучами СВ и СН , имеющими начало на ребре (АС) и перепендикулярными к нему,

т.е. L HCB = 60⁰. (см. рис.).

2) Углом между прямой и плоскостью наз-ся угол между этой прямой и её проекцией на данную плоскость, тогда углом между катетом ВС и плоскостью (САН) является L L HCB = 60⁰ .

3) Угол между гипотенузой АВ найдём, рассмотрев ΔАВН - прям.:

sin L BAH = BH/AB = 0,5√3a/(a√2) =√6/4,

таким образом L BAH = arcsin √6/4.

ОТвет: 60⁰; arcsin √6/4.

УДАЧИ

0,0(0 оценок)

Ответ:

iququwisjjs

12.04.2022 16:18

$1) \ x = \sqrt{13} \\2) \ x = \sqrt{21} \\3) x_1 = 7, x_2=x_3 = 7\sqrt{2}$

Объяснение:

Обозначим неизвестные отрезки за x

1) неизвестный отрезок является гипотенузой прямоугольного треугольника:

$x = \sqrt{3^2+2^2} = \sqrt{9+4} = \sqrt{13}$

2) неизвестный отрезок является высотой, проведённой к основанию, в равнобедренном треугольнике. Как известно, высота, проведённая к основанию, в равнобедренном треугольнике является также медианой и биссектрисой. Следовательно неизвестный отрезок делит основание пополам и является катетом в прямоугольном треугольнике с гипотенузой равной 5 и катетом равным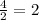 $\frac{4}{2} = 2$ :

$x = \sqrt{5^2 - 2^2} = \sqrt{25 - 4} = \sqrt{21}$

3) Здесь имеется три неизвестных отрезка, два из которых равны.

Начнём с высоты, опять же она проведена к основанию в равнобедренном треугольнике, а значит является и медианой и биссектрисой. А медиана проведённая к гипотенузе в прямоугольном треугольнике равна половине гипотенузы:

$x_1 = \frac{14}{2} = 7$

Нам известно, что оставшиеся неизвестные отрезки являются катетами в прямоугольном треугольнике и что они равны. Нам известна гипотенуза этого треугольника:

$x_2 = x_3,\\\sqrt{x_2^2+x_3^2} = 14 \\\sqrt{2x_2^2} = 14\\x_2\sqrt{2} = 14\\x_2 = \frac{14}{\sqrt{2} } = \frac{14\sqrt{2} }{2} = 7\sqrt{2}$