Есть вот такое замечательное соотношение. В итоге получается:
1+ 16/25= 1/ sin²(x)
41/25= 1/sin²(x)
25/41= sin²(x)
sin(x)= ±√25/41
ctg =4/5 , он положителен, а положителен он в 1 и 3 четвертях. По условию угол острый, то есть меньше 90 градусов, то есть подходит 1 четверть, т.к в 3 четверти угол будет лежать в промежутке (180°;270°) и считаться тупым. В 1 четверти синус положителен, то есть ответ sin(x)=√25/41
ответ:sina=5
Объяснение:
Объяснение:
Есть вот такое замечательное соотношение. В итоге получается: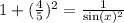
1+ 16/25= 1/ sin²(x)
41/25= 1/sin²(x)
25/41= sin²(x)
sin(x)= ±√25/41
ctg =4/5 , он положителен, а положителен он в 1 и 3 четвертях. По условию угол острый, то есть меньше 90 градусов, то есть подходит 1 четверть, т.к в 3 четверти угол будет лежать в промежутке (180°;270°) и считаться тупым. В 1 четверти синус положителен, то есть ответ sin(x)=√25/41