два туриста одновременно вышли из лагеря. Первый ехал верхом на лошади на север со скоростью 8 км/ч. второй ехал на велосипеде на запад со скоростью 6 км/ч. Каким будет расстояние между ними через 4 часа пд
В равнобедренном треугольнике АВС <BAC=<BCA=(180°-108°):2=36°. <BAD=18°, так как AD - биссектриса. Треугольник СЕD подобен треугольнику АВС, так как <DEC=108° (B треугольнике АDE <ADE=90°, <DAE=18°, a <DEA=72°. Тогда <DEC=108° как смежный с <DEA). Проведем KD параллельно АС. Тогда треугольник BKD подобен АВС и <BKD=36°. Отсюда <AKD=144°, как смежный с <BKD, а <KDA=18° (в треугольнике АКD по сумме углов треугольника: 180-144-18 = 18). Следовательно, треугольник АКD равнобедренный и АК=КD. Но АК=DC (так как АВ=ВС, а ВК=ВD). Значит и КD=DC. Тогда треугольники КВD и СЕD равны по стороне и двум прилежащим к ней углам. Отсюда ВD=DE, что и требовалось доказать.
Рассмотрим треугольник с основанием c, боковыми сторонами a и b, и медианой к основанию m. Обозначим угол наклона медианы к основанию со стороны a, и со стороны b.
По теореме косинусов:
То есть
Предположим от противного, что медиана к основанию равна полусумме боковых сторон:
Подставив выражение для в предыдущее равенство, получим:
То есть сумма двух сторон треугольника равна его третьей стороне.
Поскольку такого треугольника не существует, следовательно исходное предположение неверно, и медиана к одной стороне треугольника не может равняться полусумме двух других его сторон.
Треугольник СЕD подобен треугольнику АВС, так как <DEC=108° (B треугольнике АDE <ADE=90°, <DAE=18°, a <DEA=72°. Тогда <DEC=108° как смежный с <DEA).
Проведем KD параллельно АС. Тогда треугольник BKD подобен АВС и <BKD=36°. Отсюда <AKD=144°, как смежный с <BKD, а <KDA=18° (в треугольнике АКD по сумме углов треугольника: 180-144-18 = 18).
Следовательно, треугольник АКD равнобедренный и АК=КD. Но АК=DC (так как АВ=ВС, а ВК=ВD). Значит и КD=DC.
Тогда треугольники КВD и СЕD равны по стороне и двум прилежащим к ней углам.
Отсюда ВD=DE, что и требовалось доказать.
Рассмотрим треугольник с основанием c, боковыми сторонами a и b, и медианой к основанию m. Обозначим угол наклона медианы к основанию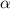 со стороны a, и
со стороны a, и 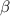 со стороны b.
со стороны b.
По теореме косинусов:
То есть
Предположим от противного, что медиана к основанию равна полусумме боковых сторон:
Подставив выражение для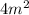 в предыдущее равенство, получим:
в предыдущее равенство, получим:
То есть сумма двух сторон треугольника равна его третьей стороне.
Поскольку такого треугольника не существует, следовательно исходное предположение неверно, и медиана к одной стороне треугольника не может равняться полусумме двух других его сторон.