Уравнение окружности в общем виде: ( х - а)^2 + (у - в)^2 = R^2, где (а,в) - координаты центра окружности, R - радиус. Если центр окружности лежит на биссектрисе, значит координаты равны у = х. Пусть у = х = t. Точка (1; 8) принадлежит окружности, значит: (1-t)^2 + (8-t)^2 = 5^2; 1 - 2t + t^2 + 64 - 16t + t^2 = 25; 2t^2 - 18t + 40 = 0; t^2 - 9t + 20 = 0; t = 4 или t = 5, уравнений, удовлетворяющих данному условию два: (х - 5)^2 + (y - 5)^2 = 5^2 или (х -4)^2 + (y - 4)^2 = 5^2
( х - а)^2 + (у - в)^2 = R^2,
где (а,в) - координаты центра окружности,
R - радиус.
Если центр окружности лежит на биссектрисе, значит координаты равны у = х. Пусть у = х = t.
Точка (1; 8) принадлежит окружности, значит:
(1-t)^2 + (8-t)^2 = 5^2;
1 - 2t + t^2 + 64 - 16t + t^2 = 25;
2t^2 - 18t + 40 = 0;
t^2 - 9t + 20 = 0;
t = 4 или t = 5,
уравнений, удовлетворяющих данному условию два:
(х - 5)^2 + (y - 5)^2 = 5^2 или (х -4)^2 + (y - 4)^2 = 5^2
Обозначим пирамиду МАВС, МО - высота пирамиды. МО перпендикулярна основанию пирамиды.
О - центр описанной окружности около основания АВС данной пирамиды.
Все углы правильного треугольника равны 60°. По т.синусов радиус АО описанной окружности равен
R=AO:2sin60°
Если условие задано верно и сторона основания равна 4, то:
Тогда по т.Пифагора из прямоугольного ∆ АМО высота
МО=√(AM²-AO²)=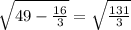
Но эта задача обычно задается со стороной основания, равной 4,5
Тогда условие задачи: В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания 4,5. Найдите высоту.
Для этого значения
R=4: 2√3/2=4,5:√3=1,5•√3
По т.Пифагора высота пирамиды
МО=√(МА²-АО²)=√(49-2,25•3)=6,5 (ед. длины)