Косинус острого угла А треугольника АВС равен корень 3√11:5. Найдите sinA

Для любого треугольника справедлива теорема синусов, которая говорит о следующем:

A/sin(a)=B/sin(b)=C/sin(c)=2R, где:

A/sin(a)=B/sin(b)=C/sin(c) - соотношения сторон треугольников к синусу противоположных им углов;

R - радиус окружности, описанной около треугольника.

1). Имеем сторону треугольника 3 (см) и противоположный ей угол, равный 120°. Тогда по теореме синусов:

3/sin(120°)=2R;

3/sin(90°+30°)=2R;

3/cos30°=2R;

3/(√3/2)=2R;

6/√3=2R;

R=3/√3; | освободимся от иррациональности, домножим и числитель, и знаменатель на √3

R=√3.

2). Аналогично, имеем сторону 3 см и угол, равный 30:

3/sin(30°)=2R;

3/(1/2)=2R;

6=2R;

R=3.

3). Аналогично, имеем сторону 3 см и угол, равный 135°;

3/sin(135°)=2R;

3/sin(90°+45°)=2R;

3/cos45°=2R;

3/(√2/2)=2R;

6/√2=2R;

R=3/√2; | освободимся от иррациональности, домножим и числитель, и знаменатель на √2

R=(3*√2)/2.

ответ: 1). R=√3; 2). R=3; 3). R=(3*√2)/2.

ответ: 13

Пошаговое решение:

1) Если один из углов прямоугольного треугольника равен 60°, тогда его второй острый угол будет равен 30°.

2) Катет, лежащий против угла 30°, равен половине гипотенузы, т.к. синус угла 30° = 0.5, а в прямоугольном треугольнике синус угла - это отношение противолежащего ему катета к гипотенузе.

3) Катет, лежащий против угла 60°, равен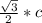 , где - гипотенуза.

4) Площадь прямоугольного треугольника равна полупроизведению его катетов. Отсюда: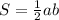 . Получаем уравнение:

Так как катет, прилежащий к углу 60°, равен половине гипотенузы (), то он равен 13.