МАКСИМУМ С пояснениями и оформлением(найти и дано, чертеж)
Длина стороны ромба АВСД равна 7 см, длина диагонали ВД= 10 см. Через
точку О пересечения диагоналей ромба проведена прямая ОК,
перпендикулярная его плоскости. Найти расстояние от точки К до вершин
ромба, если ОК= 4 см.
ответ: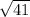 см, 2
см, 2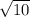 см
см
Объяснение: Смотрите рисунок
ВО = 10/2=5 см - это половина диагонали.
В прямоугольном треугольнике ВОМ по Пифагору, расстояние от точки К до вершин В и Д будет
ВK^2 = 5^2+4^2 = 25+16 = 41
Тогда ВК=КД =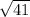 см
см
Найдем АО. Диагонали ромба перпендикулярны, поэтому треугольник АОВ прямоугольный и сторона = 7 см - гипотенуза.
По Пифагору AO^2 = 7^2 - 5^2 = 49 -25 = 24
расстояние от точки К до точек А и С будет
АК^2 = AO^2 + OK^2 = 24 + 16 = 40
Тогда АК = СК =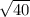 = 2
= 2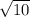 см
см