На рисунке изображены пересекающиеся плоскости альфа и бетта. Точки А и В принадлежат плоскости альфа, а точка С лежит в плоскости бетта. Скопируйте рисунок и изобразите на нем точку Д, принадлежащую плоскости бетта так, чтобы отрезки АД и ВС оказались пересекающимися

Показать ответ

Ответ:

shkiper15555

20.03.2020 03:01

Формула вычисления длины окружности, зная радиус окружности: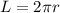 $L = 2\pi r$

Для начала определим вид треугольника.

Нам уже дано, что около трапеции однозначно описана окружность.

А окружность можно описать только около равнобедренной трапеции!.

Что и означает, что боковые стороны равны — 6; 6.

Другого выбора у нас нет, кроме как объявить, что одно из оснований ровно боковой стороне — 6, а второе основание равно: 12.

Формула вычисления радиусa описанной окружности около равнобёдренной трапеции — такова:

$R = \frac{adc}{4\sqrt{p(p-a)(p-d)(p-c)}}\\p = \frac{a+d+c}{2}$

Тоесть, для вычисления этого радиуса — нам должны быть известны основания трапеции, боковая сторона, и! диагональ.

Обозначения сторон: боковые равные стороны равны: "c"; большее основание равно: "b"; меньшее основание равно: "b".

Формула вычисления диагонали равнобедренной трапеции такова: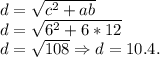 $d = \sqrt{c^2+ab}\\d = \sqrt{6^2+6*12}\\d = \sqrt{108} \Rightarrow d = 10.4.$

А в этой формуле, переменные таковы: обе боковые стороны обозначаются как "a"; верхнее основание, которое равно боковой стороне — обозначается как "b"; основание с длиной в 12 см — обозначается как "c".

Теперь, зная все стороны трапеции, и диагональ — найдём радиус: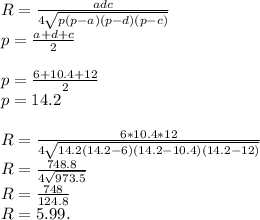 $R = \frac{adc}{4\sqrt{p(p-a)(p-d)(p-c)}}\\p = \frac{a+d+c}{2}\\\\p = \frac{6+10.4+12}{2}\\p = 14.2\\\\R = \frac{6*10.4*12}{4\sqrt{14.2(14.2-6)(14.2-10.4)(14.2-12)}}\\R = \frac{748.8}{4\sqrt{973.5}}\\R = \frac{748}{124.8}\\R = 5.99.$

Теперь, зная радиус — найдём длину окружности:

$L = 2\pi r\\L = 2*3.1415*5.99\\L = 37.63.$

Вывод: L = 37.63.

0,0(0 оценок)

Ответ:

SorrySorry

13.02.2022 22:08

библиотека

материалов ДОБАВИТЬ В ИЗБРАННОЕ

Кратко план урока

Раздел плана:

Мифы народов мира.Урок русской литературы №5

Школа: КГУ «Березняковская СОШ»

Дата:22.06.2018

Ф.И.О. учителя: Кириллова Любовь Георгиевна.

Класс: 6

Количество присутствующих:

Количество отсутствующих:

Тема урока

Библейская мифология. Миф о Вавилонской башне.

Цели обучения, обучения, которые необходимо достичь на данном уроке

6. ПО 2 -иметь общее представление о художественном произведении, понимать главную и второстепенную информацию;

6. ПО 5 -пересказывать (кратко, подробно) содержание произведения небольшой эпической или драматической формы, выражая своё мнение о героях и событиях;

6.ОС 1- участвовать в обсуждении произведения, оценивая поступки главных героев;

Цели обучения учащихся

Все учащиеся смогут: иметь общее представление о художественном произведении, понимать главную и второстепенную информацию

Большинство учащихся смогут: -пересказывать (кратко, подробно) содержание произведения небольшой эпической или драматической формы, выражая своё мнение о героях и событиях

Некоторые учащиеся смогут: участвовать в обсуждении произведения, оценивая поступки главных героев;

Критерии jwtоценивания

Отвечает на вопросы по прослушанному тексту, выделяет ключевые слова.

Строит монолог-рассуждение на заданную тему, включая основную информацию и детали.

Языковая цель:

Учащиеся могут использовать в речи ключевые слова и фразы, описывать картину, аргументировать ответы.

Ключевые слова и фразы:

Вавилон, Вавилонская башня, один язык, разные языки,взаимопонимание, разные кирпичи, непонимание, конфликт.

Полезные фразы для диалога:

По-моему..., Я думаю, что,...,для успешного взаимопонимания, причины непонимания, причины конфликта,Возможно.., Думается..., Хочется верить

Межпредметные связи

Предусматривается возможность для установления межпредметных связей с уроками истории, .географии ,самопознания, изобразительного искусства..

Использование ИТК

Интерактивная доска, интернет-ресурсы.

Предыдущее обучение:

Тема: Тюрская мифология. Миф о создании мира

План

Планируемое время 40 мин.

Запланированные задания

Ресурсы

Начало урока

10 мин.

Середина урока

20 минут

Приветствие.Пожелание друг другу успехов на уроке. Повторение в в кругу материала урока с использованием приема«Пересказ по кругу…» Миф о создании мира».Каждый учащийся говорит по 1 высказыванию.

Мотивация к изучению новой темы

Прием « Ребус»

(повторить сведения из изученного раздела«Мифы народов мира») Названия слов прикрепляем на доску.Некоторые буквы выделены красным цветом.

1.Космическое пространство (Вселенная)

2.Герой,совершивший 12 подвигов(Геракл)

3.Эти люди в древности называли себя словене(славяне)

4.Государство,где жил Геракл (Греция)

5.Священная книга христиан (Библия)

6. Мифический герой,подаривший людям огонь (Прометей)

7.Источник света и тепла (Солнце)

-Какое ключевое слово из выделенных букв прочтете?(Вавилон)

Речь сегодня пойдет о том, что означает это слово и как оно связано с нашей темой урока..

Рассказ подготовленного ученика по картине художника Питера Брейгеля с использованием интерактивной доски

hello_html_m49e2ba0f.jpg

Это одно из самых выдающихся сооружений Древнего Вавилона, а ее название и поныне является символом сумятицы и беспорядка. Согласно библейскому сюжету, Вавилонская башня рухнула. Но башня, созданная воображением Брейгеля, до сих пор стоит. На ее ярусах строители по-прежнему ведут свою неустанную работу. Привычной и повседневной жизнью живет изображенный на картине густонаселенный город… При раскопках в Вавилоне немецкому ученому Роберту Кольдевею удалось обнаружить фундамент и руины башни. Подсчёты позволяют говорить о том, что для возведения этой башни было использовано около 85 млн. кирпичей. Монументальная лестница вела к верхней платформе башни, где устремлялся в

0,0(0 оценок)

Популярные вопросы: Геометрия