Нарисуй треугольник ABC и проведи ED ∥ CA. Известно, что:
D∈AB,E∈BC, ∢ABC=65°, ∢EDB=31°.

Найди ∡ BCA.

∢BCA=
°.

Показать ответ

Ответ:

daniilznanija0

25.04.2023 13:34

1. Могут.

2. б) 6 см

3. б) 45°

Объяснение:

1. Пересекающиеся прямые а и b задают плоскость α. Прямые а и с скрещивающиеся, значит прямая с не лежит в плоскости α.

Прямые с и b могут быть параллельными.

а) Так как точки М и N принадлежат плоскости трапеции и плоскости α, то MN - линия пересечения плоскостей.

MN - средняя линия трапеции, значит

AD║MN, ⇒ AD║α (если прямая параллельна некоторой прямой, лежащей в плоскости, то она параллельна плоскости).

б)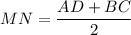 $MN=\dfrac{AD+BC}{2}$

AD + BC = 2MN

BC = 2MN - AD = 2 · 8 - 10 = 16 - 10 = 6 см

3. Признак скрещивающихся прямых: если одна прямая лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то прямые скрещивающиеся.

а) ВС лежит в плоскости (АВС),

МА пересекает (АВС) в точке А,

А не лежит на прямой ВС, значит

МА и ВС скрещивающиеся.

б) ∠(МА, AD) = 45° по условию,

BC║AD, значит

∠(МА, ВС) = 45°

(с чертежами) . 1. прямые а и b пересекаются. прямая с является скрещивающейся с прямой а. могут ли

0,0(0 оценок)

Ответ:

katyymii

22.05.2020 03:04

Для нахождения площади равнобедренного треугольника нужно умножить его основание на его высоту.

1. если треугольник равнобедренный, значит его боковые стороны равны. следовательно, мы можем вычислить длину основания
BC = 64 - (17 + 17)
ВС = 30

2. зная длину основания, мы можем найти высоту. для этого возьмем прямоугольный треугольник ADC, и воспользуемся свойством пифагора (квадрат гипотенузы равен сумме квадратов катетов):
$AC^{2} = DC^{2} + AC^{2}$
$17^{2} = 15^{2} + AD^{2}$
$AD = \sqrt{17^{2} - 15^{2}}$
AD = 8

3. найдем площадь равнобедренного треугольника как произведение высоты на основание
8 * 30 = 240
Периметр равнобедренного треугольника равен 64, а боковая сторона 17. найдите площадь треугольника