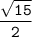Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны. Итак, в трапеции АВСД один из углов при боковой стороне СД=135°. Сумма углов, прилежащих к одной стороне трапеции, равна 180. Следовательно, угол СДА=45° Опустим из С к основанию АД перпендикуляр СН. Треугольник СНД - равнобедренный прямоугольный, т.к. угол НСД равен 90°-45°=45° Длина катетов равнобедренного прямоугольника равна половине длины гипотенузы, умноженной на √2. Или, кому привычнее, можно найти по т.Пифагора. Отсюда катеты этого треугольника равны 8,5√2 ВН₁=СН как равные перпендикуляры между параллельными прямыми. В треугольнике ВАН₁ ∠ ВАН=∠АВС=30°, как накрестлежащий при пересечении параллельных прямых секущей. ВН₁=8,5√2 АВ=ВН₁:sin(30°) АВ=17√2
Итак, в трапеции АВСД один из углов при боковой стороне СД=135°.
Сумма углов, прилежащих к одной стороне трапеции, равна 180. Следовательно, угол СДА=45°
Опустим из С к основанию АД перпендикуляр СН.
Треугольник СНД - равнобедренный прямоугольный, т.к. угол НСД равен 90°-45°=45°
Длина катетов равнобедренного прямоугольника равна половине длины гипотенузы, умноженной на √2.
Или, кому привычнее, можно найти по т.Пифагора.
Отсюда катеты этого треугольника равны 8,5√2
ВН₁=СН как равные перпендикуляры между параллельными прямыми.
В треугольнике ВАН₁ ∠ ВАН=∠АВС=30°, как накрестлежащий при пересечении параллельных прямых секущей.
ВН₁=8,5√2
АВ=ВН₁:sin(30°)
АВ=17√2
Дано: AB=1; AC=√15; BM=MC; AM=2.
Найти: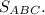
A₁ ∈ AM; AM=A₁M
ABA₁C - параллелограмм т.к. диагонали делятся точкой пересечения пополам (BM=MC по условию; AM=MA₁ по построению), поэтому A₁C=AB=1.
ΔAA₁C - прямоугольный т.к. выполняется теорема Пифагора:
AA₁² = (2AM)² = (2·2)² = 4² = 16;
AC²+CA₁² = (√15)²+1² = 15+1 = 16;
16 = 16 ⇒ AA₁² = AC²+CA₁².
Поэтому ∠ACA₁ = 90°, он лежит на против гипотенузы AA₁.
ABA₁C - прямоугольник т.к. это параллелограмма с углом в 90° (∠ACA₁=90°), поэтому ∠BAC=90°.
ответ: