Острый угол между диагоналями прямоугольника равен a , а сторона которая лежит против этого угла, - a. найдите вторую сторону прямоугольника.ответы а) tg (a/2)в)a/tg(a/2)г) a tg (a/2)

Показать ответ

Ответ:

Kyrylo13

14.09.2020 09:07

***

дано:

прямоугольный треугольник АСВ

CH - высота

СN - медиана

CH + CN = 79 см

АС+СВ=70 см

найти - периметр

медиана это отрезок который соединяет вершину треугольника с серединой противоположной стороны.медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы. $m=\frac{1}{2} \cdot c$ где м - медиана, с - гипотенуза.

следовательно:

$CN = \frac{1}{2} \cdot AB$

высота это перпендикуляр, который опущен из вершины треугольника на противоположную сторону.св. синуса острого угла в прям. треугольнике => $h=\frac{ab}{c}$ где а и b катеты прямоугольного треугольника, с - гипотенуза

следовательно:

$CH = \frac{AC\cdot CB}{AB}$

CH + CN = 79 см - по условию,

значит:

$\frac{1}{2} \cdot AB + \frac{AC\cdot CB}{AB} = 49$

$\frac{AB^2+2AC\cdot BC}{2AB} =49\\$

$AB^2 +2\cdot AC\cdot BC= 98AB$

по теореме Пифагора:

сумма квадратов длин катетов равна квадрату длины гипотенузы. c^2=a^2+b^2

следовательно:

AB^2 = AC^2 +CB^2

$AC^2+CB^2 +2AC\cdot CB=98AB$

=> << (a+b)^2=a^2+2ab+b^2 >>

$(AC+CB)^2=98AB\\$

$AC+CB=70\\$

$= \\$

98AB=70^2

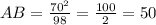
$AB=\frac{70^2}{98} =\frac{100}{2} =50$

периметр треугольника равен сумме длин всех его сторон. P=a+b+c, где a, b, c - стороны

AB = 50

AC + CB = 70

P= AC+CB+AB = 70+50=120

ответ: периметр треугольника равна 120 см.

Сума катетів прямокутного трикутника дорівнює 70 см, а сума медіани і висоти, проведеної до гіпотену

0,0(0 оценок)

Ответ:

f0xsick

25.05.2020 23:01

Радиус окружности равен 7,5 см.

Объяснение:

Основание равнобедренного треугольника является хордой касающейся окружности боковых сторон треугольника. Найдите ее радиус, если стороны треугольника равны 10 см, 10 см и 12 см.

Дано: ΔАВС - равнобедренный.

Окр.О,R касается АВ и ВС;

АС - хорда;

АВ = ВС = 10 см; АС = 12 см.

Найти: R

Определимся с чертежом.

Если АС - хорда Окр.О;R, то точки А и С - точки касания окружности с АВ и ВС соответственно.

Соединим В и О.

1. Рассмотрим ΔАВС - равнобедренный.

Радиус вписанной окружности лежит на биссектрисе угла.

⇒ ВО - биссектриса.

В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.