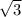От Точка O - точка пересечения медиан АА1, BB1, СС1. Пользуясь данными рисунка, найдите длину отрезка BO. В ответе укажите только число.
​

В прямоуг. треуг. против угла в 30° лежит катет, равный  половине гипотенузы, т.е. в ΔАВС против угла В лежит катет АС, пусть он равен х, тогда гипотенуза АВ = 2х, а биссектриса является средним пропорциональным между отрезками, на которые она разбивает сторону СВ, т.е. КС/КВ=АС/АВ, КС пусть равен у, тогда КВ равен (18-у), Значит, у/(18-у)=1/2. Или по основному свойству пропорции произведение крайних равно произведению средних членов, т.е. 2у=18-у.

Или 3у=18, откуда у=6. КС =6, значит, АК, как гипотенуза в треуг. АСК в два раза больше, чем катет СК, лежащий против угла в 30°, т.к. ∠КАС =(1/2)*угла САВ, равного 60°. Поэтому АК = 12.

ответ Биссектриса равна 12.

1. Катет 1 - длина х

катет 2 - длина (x-10)

гипотенуза - длина (х+10)

Правило прямоугольного треугольника:

х^2 + (x-10)^2 = (x+10)^2

x^2 + x^2 - 2*10*x + 100 = x^2 + 2*10*x + 100

2x^2 - 20x=x^2 + 20x

2x-20 = x+20

x=40

Катет 1 = 40, катет 2 = 30, гипотенуза = 50.

2. Разделим получившийся треугольник с вершиной с углом 120 градусов высотой на два треугольника. Получим прямоугольный треугольник с катетами, равными половинам сторон прямоугольника. При этом известна длина меньшего катета: 4/2=2 и примыкающий угол а=120/2=60 градусов. Больший катет равен: 

2*tg60=2*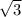

Площадь прямоугольника: 4*2*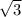 = 8*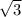

ответ: 8*