Параллелограмм вертикального параллелепипеда с основанием 6 см, 10 см и углом 60 градусов. Если высота параллелепипеда 5 см, найдите диагонали этого параллелепипеда.
Две окружности ,вписанные в угол ,касаются друг друга внешним образом .Центральный угол в 120° большей окружности , составленный из радиусов проведенных в точки касания ,стягивает дугу 15 см. Найти длину малой окружности.
Объяснение:
Пусть ОА=ОМ=R , CM=CK=r . По формуле длины дуги ,
⇒ R= см. По свойству отрезков касательных ∠АОР=60° .
Пусть СН⊥ОА , тогда ∠НСО=30°.
В ΔНСО по свойству угла 30° : ОС=2*ОН , но ОС=R+r , ОН=R-r ,
Объяснение:
у=4х-7
Точка А имеет координаты (8,2;25,8), где абсцисса х=8,2.
ордината у=25,8.
Подставим значение х и у в график, и проверим уравнивается правая и левая часть.
25,8=4*8,2-7
25,8=32,8-7
25,8=25,8
Точка А(8,2;25,8) принадлежит графику у=4х-7
2)
т.В(-71;-290)
х=-71
у=-290
у=4х-7, подставляем значение х и у.
-290=4(-71)-7
-290=-284-7
-290≠291
Правая и левая часть не уравнялись, значит т.В(-71;-290) не принадлежит этому графику.
3) т.С(35;-133)
х=35
у=-133
у=4х-7, подставляем значение х и у.
-133=4*35-7
-133=140-7
-133≠133
т.С не принадлежит графику у=4х-7.
4) т.D(-46;-191)
x=-46
у=-191
у=4х-7
-191=4(-46)-7
-191=-184-7
-191=-191
т.D(-46;-191) принадлежит этому графику.
Бог в
Две окружности ,вписанные в угол ,касаются друг друга внешним образом .Центральный угол в 120° большей окружности , составленный из радиусов проведенных в точки касания ,стягивает дугу 15 см. Найти длину малой окружности.
Объяснение:
Пусть ОА=ОМ=R , CM=CK=r . По формуле длины дуги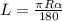
,
Пусть СН⊥ОА , тогда ∠НСО=30°.
В ΔНСО по свойству угла 30° : ОС=2*ОН , но ОС=R+r , ОН=R-r ,
тогда R+r=2(R-r) → r=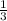
*R → r= 
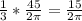(см) .
Длина окружности С=2πr , тогда С=2π*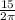
=15 (см) .