Дано: ABCD - трапеция, , в ABCD вписана окружность l, точка К принадлежит l (), АК=20 см, KD=25 см.
Найти:
Решение: Пусть О - центр окружности l. Заметим, что диаметр окружности равен высоте трапеции. Построим перпендикуляр к стороне АВ от центра О окружности. Назовем его ОМ. Заметим, что АКОМ - квадрат. Все углы у него прямые, ОМ=ОК по построению. Значит ОК=АК=20 см. Значит АВ=2ОК=40 см.
По свойству четырехугольников, описанных вокруг окружности
AD+BC=AB+CD (*)
AD=AK+KD=20+25=45 см.
Подставим в (*) то, что известно
45+ВС=40+CD
BC=CD-5. (**)
Если из вершины С опустить высоту Т на основание AD, то можно рассмотреть прямоугольный треугольник CTD. CT=AB потому что, АВСТ - прямоугольник. Все углы прямые. Значит СТ=АВ=40 см. По построению TD=AD-AT=45-AT. AT=BC - по свойству прямоугольника. Пусть TD=x см.
Треугольник CTD - является прямоугольным по построению, так как
По теореме Пифагора
Подставим известные данные и обозначения в последнюю формулу
Подставим CD в формулу (**)
BC=AD-TD=45-x - подставляем в верхнюю формулу
Возведем в квадрат обе части
2500-100x=1600
100x=2500-1600
100x=900
x=9 см
Значит TD=9 см, AT=AD-TD=45-9=36 cм. Так как по свойству прямоугольника АВСТ ВС=АТ=36 см.
по теореме косинусов a²=b²+c²-2bccosA cosA=(b²+c²-a²)/2bc=804/924=67/77
sin²A=1-cos²A=1440/77²=36*40/77² sinA=4*√40/77
b²=a²+c²-2accosB cosB=(a²+c²-b²)/2ac=164/484=41/121 cosB=cos2*(B/2)
=cos²B/2-sin²B/2=1-2sin²(B/2) sin²B/2=(1-cosB)/2=40/121 sin(B/2)=√40/11
по теореме синусов:
BD/sinA=c/sinα=AD/sin(B/2)
BD/sinC=a/sin(180-α)=DC/sinB/2
берем вторые равенства и складываем sin(180-α)=sinα
(с+a)/sinα=(AD+DC)/sin(B/2)=b/sin(B/2)
sinα=(c+a)*sin(B/2)/b=33*√40/11*21=√40/7
по теореме синусов
с/sinα=BD/sinA
BD=c*sinA/sinα=22*4*√40*7/(77*√40)=8
Дано: ABCD - трапеция,
, в ABCD вписана окружность l, точка К принадлежит l (
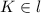), АК=20 см, KD=25 см.
Найти:
Решение: Пусть О - центр окружности l. Заметим, что диаметр окружности равен высоте трапеции. Построим перпендикуляр к стороне АВ от центра О окружности. Назовем его ОМ. Заметим, что АКОМ - квадрат. Все углы у него прямые, ОМ=ОК по построению. Значит ОК=АК=20 см. Значит АВ=2ОК=40 см.
По свойству четырехугольников, описанных вокруг окружности
AD+BC=AB+CD (*)
AD=AK+KD=20+25=45 см.
Подставим в (*) то, что известно
45+ВС=40+CD
BC=CD-5. (**)
Если из вершины С опустить высоту Т на основание AD, то можно рассмотреть прямоугольный треугольник CTD. CT=AB потому что, АВСТ - прямоугольник. Все углы прямые. Значит СТ=АВ=40 см. По построению TD=AD-AT=45-AT. AT=BC - по свойству прямоугольника. Пусть TD=x см.
Треугольник CTD - является прямоугольным по построению, так как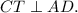
По теореме Пифагора
Подставим известные данные и обозначения в последнюю формулу
Подставим CD в формулу (**)
BC=AD-TD=45-x - подставляем в верхнюю формулу
Возведем в квадрат обе части
2500-100x=1600
100x=2500-1600
100x=900
x=9 см
Значит TD=9 см, AT=AD-TD=45-9=36 cм. Так как по свойству прямоугольника АВСТ ВС=АТ=36 см.
Теперь осталось вычислить СD. По формуле (**)
36=СD-5
СD=36+5
СD=41 см.
=86+36+40=122+40=162 см.
ответ:
см
_________________________________________________________________________
Отвечаю на Ваш вопрос по решению примера по алгебре.
Упростим выражение