Если прямая (DC), параллельна какой-нибудь прямой (AB), расположенной в плоскости (α), то она параллельна самой плоскости. Если плоскость проходит через прямую (DC), параллельную другой плоскости (α), и пересекает эту плоскость, то линия пересечения (EF) параллельна первой прямой (DC). Расстояние от прямой DC до плоскости α - это перпендикуляр из любой точки этой прямой на плоскость α. Итак, в прямоугольном треугольнике АЕD катет АЕ равен по Пифагору АЕ=√(AD²-DE²)=√(36²-18²)=18√3. Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения. То есть угол между плоскостью α и плоскостью квадрата - это угол EAD, cинус которого равен отношению противолежащего катета к гипотенузе: Sinβ=ED/AD=18/36=1/2. Значит угол между плоскостями равен 30°. Площадь проекции квадрата на плоскость α - это площадь прямоугольника AEFB, равная S=AB*AE=36*18√3=648√3см²
Для ответа на заданный вопрос нужно найти, какую часть от целого круга составляет сектор с центральным углом, равный данным дугам. Такова же будет и часть площади, которую этот сектор занимает в круге.
Чтобы вычислить, какую часть целого числа составляет другое число, нужно представить ответ в виде правильной дроби. Записываем искомую величину над дробной чертой, как числитель а целое - под ней ( знаменатель). Желательно по возможности ( и для наглядности) сократить дробь (то есть разделить числитель и знаменатель на общий множитель.
а)
Какую часть от целого круга составляют оставшиеся три сектора и сектор с любой градусной мерой центрального угла, Вы без труда найдете самостоятельно.
Углы данной величины чаще всего встречаются в задачах по геометрии, и их доля от общего круга запоминается наизусть.
Расстояние от прямой DC до плоскости α - это перпендикуляр из любой точки этой прямой на плоскость α.
Итак, в прямоугольном треугольнике АЕD катет АЕ равен по Пифагору
АЕ=√(AD²-DE²)=√(36²-18²)=18√3.
Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения. То есть угол между плоскостью α и плоскостью квадрата - это угол EAD, cинус которого равен отношению противолежащего катета к гипотенузе: Sinβ=ED/AD=18/36=1/2. Значит угол между плоскостями равен 30°.
Площадь проекции квадрата на плоскость α - это площадь прямоугольника AEFB, равная S=AB*AE=36*18√3=648√3см²
Площадь полного круга занимает все его 360°.
Для ответа на заданный вопрос нужно найти, какую часть от целого круга составляет сектор с центральным углом, равный данным дугам. Такова же будет и часть площади, которую этот сектор занимает в круге.
Чтобы вычислить, какую часть целого числа составляет другое число, нужно представить ответ в виде правильной дроби. Записываем искомую величину над дробной чертой, как числитель а целое - под ней ( знаменатель). Желательно по возможности ( и для наглядности) сократить дробь (то есть разделить числитель и знаменатель на общий множитель.
а)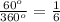
Какую часть от целого круга составляют оставшиеся три сектора и сектор с любой градусной мерой центрального угла, Вы без труда найдете самостоятельно.
Углы данной величины чаще всего встречаются в задачах по геометрии, и их доля от общего круга запоминается наизусть.