Теореме о неравенстве треугольника каждая сторона треугольника меньше суммы 2 других углов. есть ошибка. какая? 1)вместо углов должно быть сторон 2) не каждая а одна и только одна 3)не треугольника а равнобедренного треугольника 4) не меньше а больше 5) не суммы а произведения

Показать ответ

Ответ:

kravchenjatkop00zs0

17.10.2020 15:23

Для любой правильной призмы справедливы формулы:

Площадь боковой поверхности:

Sбок = Pосн · h, где

Росн - периметр основания,

h - высота.

Площадь полной поверхности:

Sполн = Sбок + 2Sосн

Объем:

V = Sосн · h

____________________

a - сторона основания.

____________________

Правильная треугольная призма:

в основании лежит правильный треугольник, значит

Sосн =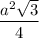 $\dfrac{a^{2}\sqrt{3}}{4}$

Sбок = 3а · h

Sполн = 3a · h + 2 · a²√3/4 = 3ah + a²√3/2

$V=\dfrac{a^{2}\sqrt{3}}{4}\cdot h$

____________________

Правильная четырехугольная призма:

в основании - квадрат, значит

Sосн = a²

Sбок = 4ah

Sполн = 4ah + 2a²

V = a²h

____________________

Правильная шестиугольная призма:

Sосн =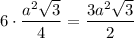 $6\cdot \dfrac{a^{2}\sqrt{3}}{4}=\dfrac{3a^{2}\sqrt{3}}{2}$

Sбок = 6ah

Sполн = 6ah + 2 · 3a²√3/2 = 6ah + 3a²√3

$V=\dfrac{3a^{2}\sqrt{3}}{2}\cdot h$

0,0(0 оценок)

Ответ:

Marina12971

01.04.2020 15:49

На сторонах угла∡ABC точки A и C находятся в равных расстояниях от вершины угла BA=BC. Через эти точки к сторонам угла проведены перпендикуляры AE⊥BA CD⊥BC.

1. Чтобы доказать равенство ΔAFD и ΔCFE, докажем, что ΔBAE и ΔBCD, по второму признаку равенства треугольников:

BA=BC

∡BAF=∡BCF=90°

∡ABC — общий.

В этих треугольниках равны все соответсвующие эелементы, в том числе BD=BE, ∡D=∡E.

Если BD=BE и BA=BC, то BD−BA=BE−BC, то есть AD=CE.

Очевидно равенство ΔAFD и ΔCFE также доказываем по второму признаку равенства треугольников:

AD=CE

∡DAF=∡ECF=90°

∡D=∡

Подробнее - на -

Объяснение: