Допустим дана трапеция ABCD, угол ВАС - прямой, биссектриса проведена из угла CDA, АВ=12см, CD=15см. Т.к. биссектриса делит угол пополам, то угол СDB равен углу BDA.
Угол BDA равен углу DBC как накрестлежащий. Следовательно CDB=BDA=DBC. Значит треугольник DBC - равнобедренный и сторона CD равна стороне BC, значит BC=15 см.
Проведем высоту СН к основанию AD. Т.к. трапеция прямоугольная CH=AD=12см. У нас получился прямоугольный треугольник CHD, в котором известно CH=12см, CD=15см.
Нужно найти катет HD.
Используем формулу для нахождения гипотенузы в прямоугольном треугольнике
Т.к. ABCH - прямоугольник, то ВС=АH=15см. Из этого следует, что AD=15+9=24. Т.к. трапеция прямоугольная, то сторона AB - высота.
Объяснение:
Дано: АВСD- трапеция,АВ=12 см,СD=15 см
Найти:S-?
AB=h=CH=12 см
DH=√CD²-CH²=√15²-12²=√225-144=√81=9 см
sin(D)=CH/CD=12/15=4/5=0,8
<D=53°
<BDA=1/2<D=1/2×53°=26,5°
<ABD=90°-<BDA=90°-26,5°=63,5°
AD=AB×tg63,5=12×2,0056≈24 см
BC=AD-DH=24-9= 15 см
S =(AD+BC)÷2×AB=(24+15)÷2×12= 234 см²
234
Объяснение:
Допустим дана трапеция ABCD, угол ВАС - прямой, биссектриса проведена из угла CDA, АВ=12см, CD=15см. Т.к. биссектриса делит угол пополам, то угол СDB равен углу BDA.
Угол BDA равен углу DBC как накрестлежащий. Следовательно CDB=BDA=DBC. Значит треугольник DBC - равнобедренный и сторона CD равна стороне BC, значит BC=15 см.
Проведем высоту СН к основанию AD. Т.к. трапеция прямоугольная CH=AD=12см. У нас получился прямоугольный треугольник CHD, в котором известно CH=12см, CD=15см.
Нужно найти катет HD.
Используем формулу для нахождения гипотенузы в прямоугольном треугольнике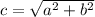
Т.к. ABCH - прямоугольник, то ВС=АH=15см. Из этого следует, что AD=15+9=24. Т.к. трапеция прямоугольная, то сторона AB - высота.
Найдем площадь трапеции по формуле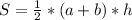
S=1/2*(15+24)*12=6*39=234