В треугольнике APM проведена высота PN.
Известно, что ∡ PAM = 28° и ∡ APM = 137°.
Определи углы треугольника NPM.

∡ PNM =
∡ NPM =
∡ PMN =

Показать ответ

Ответ:

Makeev20

23.04.2021 23:10

Центральный угол равен 94°, тоесть — противоположная ему дуга — равна 94°.

На меньшую дугу AC — опирается угол <ABC, тоесть эта же дуга равна: <ACB*2 = 70*2 = 140°.

Дуга ACB — полуокружность, тоесть: меньшая ∪CB = 180-140 = 40°.

<A — опирается на меньшую дугу ∪CB, тоесть: <A = 40/2 = 20°.

<C = 180-(20+70) = 90°.

Найти: <ACD; <AOD

Угол B — опирается на меньшую дугу AD, тоесть: ∪AD = <B*2 = 60*2 = 120°.

∪AD = 120° => <AOD = 120°.

<ACD — опирается на ту же меньшую дугу AD, тоесть: <ACD = ∪AD/2 = 60°.

0,0(0 оценок)

Ответ:

pomogitmneaaaa

01.06.2023 08:17

Стороны оснований правильной треугольной усеченной пирамиды ABCA1B1C1 равны 8 см и 5 см, а высота пирамиды - 3 см. Найдите площадь сечения пирамиды плоскостью, проходящей через прямую AB и точку C1.

Объяснение:

1) Т.к усеченная пирамида правильная , то АС₁=ВС₁. В сечении ΔАВС₁-равнобедренный треугольник .Найдем площадь по формуле Герона S= √p (p−a) (p−b) (p−c) , где p= 1 ÷2 *(a+b+c) полупериметр.

2) В равносторонних треугольниках ΔАВС, ΔА₁В₁С₁ найдем высоты , по т. Пифагора А₁Н₁=√(5²-2,5²)=√(2,5*7,5)=√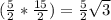 $(\frac{5}{2} *\frac{15}{2} )=\frac{5}{2}\sqrt{3}$ (см),

АН=√(8²-4²)=√(4*12)=4√3 (см).

Высота правильной усеченной пирамиды проходит через центр треугольника , поэтому радиусы вписанных окружностей равны

r₁=О₁Н₁=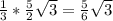 $\frac{1}{3} *\frac{5}{2}\sqrt{3}=\frac{5}{6}\sqrt{3}$ (см),

r=ОН=1/3*4√3=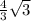 $\frac{4}{3} \sqrt{3}$ (см).

3) В прямоугольной трапеции ОО₁Н₁Н проведем высоту Н₁К. Тогда

КН=ОН-ОК=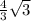 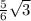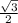$\frac{4}{3} \sqrt{3}$ - $\frac{5}{6}\sqrt{3}$ = $\frac{\sqrt{3} }{2}$ ( см)

ΔКНН₁- прямоугольный , по т. Пифагора НН₁=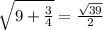 $\sqrt{9+\frac{3}{4} } =\frac{\sqrt{39} }{2}$ ( см).

4) В равнобедренной трапеции СС₁В₁В проведем высоту С₁М .

Тогда МВ=5+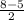 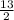$\frac{8-5}{2}$ = $\frac{13}{2}$ ( см)

ΔМС₁В-прямоугольный , по т. Пифагора

С₁В=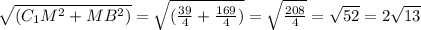 $\sqrt{(C_1M^{2} +MB^{2} )} =\sqrt{(\frac{39}{4}+\frac{169}{4} ) } =\sqrt{\frac{208}{4} } =\sqrt{52} =2\sqrt{13}$ (cм).

С₁А=2√13 см( диагонали в равных равнобедренных трапециях равны)

5) По ф. Герона

$p=\frac{8+2*2\sqrt{13} }{2} =4+2\sqrt{13} \\p-a=4+2\sqrt{13}-8 =2\sqrt{13}-4 \\p-b=4+2\sqrt{13}-2\sqrt{13} =4\\S=\sqrt{(4+2\sqrt{13} )*(2\sqrt{13}-4)*4^{2} } =4*\sqrt{(52-16)} =4\sqrt{36} =24 (cm^{2} )$ .