Висота правильної трикутної піраміди дорівнює 20 см, а двогранний кут між бічною гранню і площиною основи піраміди дорівнює 30°. Обчисли об'єм піраміди. Об'єм дорівнює
Объяснение: В ΔМNK из точки М проведите дугу окружности так, чтобы пересечь прямую NK в двух точках Р и Q. Затем поочереди из двух точек Р и Q проведите дуги одинакового радиуса на полу- плоскости относительно прямой NK, где нет точки М. Назовём точку пересечения этих дуг точкой А. Соединим М и А, получим МН ⊥ NK.
Описание: 1) окр (М; r) ∩ MK, получим Р и Q.
2) окр (Р; R) ∩ окр (К; R) = А.
3) МА ∩ NK = Н, МН- искомая высота Δ МNК.
В ΔСДР проведём поочерёдно две дуги одинаковым радиусом больше половины отрезка ДР навстречу друг другу из точек Д и Р. Эти дуги пересекутся в двух точках М и N. Соединим отрезком точки М и N.
Точку пересечения МN и ДР обозначим точкой К. Проведём отрезок СК, который и будет медианой ΔСДР.
Описание: 1)окр (Д; R) ∩ окр(Р; R), получим М и N.
2) MN ∩ ДР = К, СК- искомая медиана ΔСДР.
P.S. Если непонятно обозначение окружности в описании, то:
окр ( Р; R) - обозначение окружности с центром в Р и радиусом R.
Объяснение: В ΔМNK из точки М проведите дугу окружности так, чтобы пересечь прямую NK в двух точках Р и Q. Затем поочереди из двух точек Р и Q проведите дуги одинакового радиуса на полу- плоскости относительно прямой NK, где нет точки М. Назовём точку пересечения этих дуг точкой А. Соединим М и А, получим МН ⊥ NK.
Описание: 1) окр (М; r) ∩ MK, получим Р и Q.
2) окр (Р; R) ∩ окр (К; R) = А.
3) МА ∩ NK = Н, МН- искомая высота Δ МNК.
В ΔСДР проведём поочерёдно две дуги одинаковым радиусом больше половины отрезка ДР навстречу друг другу из точек Д и Р. Эти дуги пересекутся в двух точках М и N. Соединим отрезком точки М и N.
Точку пересечения МN и ДР обозначим точкой К. Проведём отрезок СК, который и будет медианой ΔСДР.
Описание: 1)окр (Д; R) ∩ окр(Р; R), получим М и N.
2) MN ∩ ДР = К, СК- искомая медиана ΔСДР.
P.S. Если непонятно обозначение окружности в описании, то:
окр ( Р; R) - обозначение окружности с центром в Р и радиусом R.
∠BAD+∠BCD = 180°;
∠BCA = 180°-∠BAD = 180°-120° = 60°
Вписанные углы опирающиеся на одну дугу равны.∠CAD - вписанный и опирается на ∪CD
∠CBD - вписанный и опирается на ∪CD
∠CAD = ∠CBD
По теореме синусов в треугольнике CBD: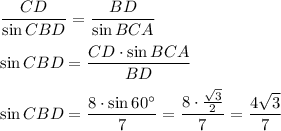
По основному тригонометрическому тождеству (sin²α+cos²α=1):Пусть BC=x, тогда 0<x<4.
Рассмотрим случай, когда cos(CBD) = 1/7По теореме косинусов в треугольнике CBD:
x²-2x-15 = 0
D = (-2)²-4·1·(-15) = 4+60 = 8²
x₁ = (2+8)/2 = 10/2 = 5
x₂ = (2-8)/2 = -6/2 = -3
Ни один корень не подходит под условие 0<x<4.
Теперь случай, когда cos(CBD) = -1/7По теореме косинусов в треугольнике CBD:
x²+2x-15 = 0
D = 2²-4·1·(-15) = 4+60 = 8²
x₃ = (-2+8)/2 = 6/2 = 3
x₄ = (-2-8)/2 = -10/2 = -5
0 < x₃ < 4
x = 3 удовлетворяет условию, значит cos(CBD) = -1/7.
cos(CBD) < 0, а sin(CBD) > 0. Поэтому ∠CBD - угол второй четверти, тогда ∠CBD = arccos(-1/7)
∠CAD = arccos(-1/7)
ответ: arccos(-1/7).