В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа будет являться число .
В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси ).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
Расцветали яблони и груши,
Поплыли туманы над рекой.
Выходила на берег Катюша,
На высокий берег на крутой.
Выходила на берег Катюша,
На высокий берег на крутой.
Выходила, песню заводила,
Про степного сизого орла.
Про того, которого любила,
Про того, чьи письма берегла.
Про того, которого любила,
Про того, чьи письма берегла.
Ой ты песня, песенка девичья,
Ты лети за ясным солнцем вслед
И бойцу на дальнем пограничье
От катюши передай привет
И бойцу на дальнем пограничье
От катюши передай приве
Пошаговое объяснение:
Пошаговое объяснение:
Точка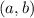
на комплексной плоскости изображает число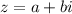 
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа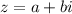
будет являться число 
.
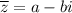В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси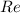
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.