30 учнів заходячи в приміщення музею зняли смос взуття. Потім вони по черзі виходять і взувають довільну пару, розміру не меншого ніж мала їх власна пара. Яка максимальна кількість учнів може залишитися без взуття потрібного розміру?

17.

1-2y=3

-2y = 3 - 1

-2y = 2 | : (-2)

y = -1

x = 1 - (-1) = 1+1 = 2

ответ: (2;-1)

18.

2 sin²x + 5 cos x + 1 = 0

Из основного тригонометрического тождества sin²x + cos²x = 1 выразим sin²x

sin²x  = 1-cos²x

2 * (1-cos²x) + 5 cos x + 1 = 0

2-2cos²x + 5 cos x + 1 = 0 | :(-1)

2cos²x - 5 cos x - 3 = 0

Пусть  cos x=t, тогда

2t² - 5t - 3 = 0

D = (-5)² - 4*2*(-3) = 25 + 24 = 29 = 7²

Вернёмся к замене:

Т.к. в уравнении cos x = a есть условие, что |a|≤1, то используем только второй корень

, n∈Z

, n∈Z

,n∈Z

,n∈Z

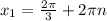ответ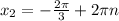: ,n∈Z ; ,n∈Z

Пошаговое объяснение:

1.

p=5/(3+5)=5/8=0,625

2.

Площадь боковой поверхности призмы:

S(бок)=P·h, где

P - периметр основания, см;

h - высота призмы, см.

Вспоминаем теорему Пифагора и вычисляем высоту призмы:

h=√(10²-6²)=√(100-36)=√64=8 см

Вспоминаем формулу периметра треугольника и вычисляем периметр основания треугольной призмы:

P=3·6=18 см

S(бок)=18·8=144 см² - площадь боковой поверхности призмы.

Объём призмы:

V=S(осн)·h, где

S(осн) - площадь основания, см².

Площадь основания призмы вычисляем, исходя из формулы площади правильного треугольника:

S(осн)=(6²√3)/4=(36√3)/4=9√3 см²

V=9√3 ·8=72√3 см³ - объём призмы.

3.

Исходя из формулы числа сочетаний, вычисляем сколькими можно выбрать 2 детали из ящика: