Делимость чисел/ Выполните тест - по теме: "Делимость чисел" 1-7 пункт в учебнике 1. Найдите все делители числа 6. 1) 1; 2; 3; 6 2) 2; 3 3) 1; 2; 3 4) 6; 12; 18 5) 6 2. Найдите все двузначные числа, кратные 22. 1) 22; 44; 66; 88 2) 22 3) 11; 22 4) 1; 2; 11; 22 5) 2; 11; 22 3. Какое из следующих чисел делится на 3? 1) 1230732 2) 521386 3) 251413 4) 1421423 5) 1237325 4. Какое из следующих чисел делится на 5? 1) 23450625 2) 3214213 3) 1232124 4) 3124123 5) 5216231 5. Найдите число, которое делится и на 9, и на 5. 1) 17325 2) 25325 3) 21213 4) 56320 5) 18981 6. Найдите число, которое делится и на 2, и на 3. 1) 21852 2) 18213 3) 18212 4) 21351 5) 32132 7. Какую цифру надо поставить вместо * в число 25132*7, чтобы это число делилось на 9? 1) 7 2) 1 3) 6 4) 8 5) 9 8. Разложите на множители число 480. 1) 2) 3) 4) 5) 9. Найдите НОД чисел и . 1) 8 2) 2 3) 1680 4) 168 5) 80 10. Найдите НОК чисел и 1) 120 2) 8 3) 2 4) 24 5) 40 11. Найдите НОД чисел 24 и 66. 1) 6 2) 11 3) 24 4) 264 5) 66 12. Найдите НОК чисел 18 и 30. 1) 90 2) 6 3) 18 4) 30 5) 540 13. Найдите НОД чисел 71 и 179. 1) 1 2) 71 3) 179 4) 12709 5) 3 14. Укажите пару взаимно чисел. 1) 7 и 47 2) 14 и 49 3) 16 и 26 4) 27 и 15 5) 15 и 36 15. Какое из чисел не является делителем числа 245? 1) 17 2) 7 3) 5 4) 49 5) 35 16. Какая из данных сумм кратна 2? 1) 24153 + 1251 2) 215010 + 11121 3) 12312 + 2121211 4) 12113 + 10010 5) 20012 + 2110113 17. Сколько натуральных чисел, кратных 3, находятся между числами 7 и 16? 1) 3 2) 2 3) 5 4) 1 5) 6 18. Сколько существует двузначных чисел, кратных 7, но не кратных 21? 1) 9 2) 8 3) 13 4) 4 5) 1 19. В упаковке 25 конфет. Сколько конфет можно взять, не вскрывая упаковку? 1) 75 2) 5 3) 15 4) 120 5) 55 20. Сколько различных пятизначных чисел, кратных 10, можно составить из цифр 0, 5, 7, 8, 9. (Цифры в числах не повторяются) 1) 24 2) 12 3) 22 4) 120 3) 4
или проще
Пошаговое объяснение:
Вспомним формулу для разложения функции в ряд Тейлора
1 Запишем функцию
2 Найдем несколько производных:
...
3 Найдем общий вид производной:
У нас в любом случае будет производная произведения, тогда наша производная распадется на какое-то количество слагаемых либо просто синуса, либо просто косинуса и слагаемое с х умноженным на либо синус, либо косинус.
Заметим, что производная синуса равна
Тогда наше произведение в зависимости от n будет иметь разный вид.
Заметим, что всего различных слагаемых без множителя х будет n штук и все они будут иметь одинаковый знак
При n одинаковой четности знак один и тот же, в данной точке функция имеет вид
(производная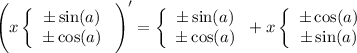
меняет местами функции)
Мы можем записать для четных n знак у функции в виде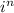
где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени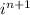 
Для функции без множителя х формула такая (учитывая значения)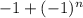
- мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
Для функции со множителем формула другая
Чтобы избавится от ненужных двоек в первом случае, умножим все на
, и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
Тогда общая формула производной имеет вид
Можем вынести множитель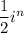
за скобки
4 Тогда запишем ряд Тейлора
Начинаю с 1 так как писалась формула производной от 1.
f(2) = 2 * cos ( 2-2 ) = 2 * 1 = 2
Это и есть ответ
а)ε= √21/5 ; A(–5;0)
a=5
ε=c/a
c=ε·a=√21
b2=a2–c2=25–21=4
О т в е т.
(x2/25)+(y2/4)=1
б)A (√80;3) ,B(4 √6 ;3 √2)
Каноническое уравнение гиперболы
(x2/a2)–(y2/b2)=1
чтобы найти а и b подставляем координаты точек А и В:
{(80/a2)–(9/b2)=1
{(96/a2)–(18/b2)=1
Умножаем первое уравнение на (–2):
{–(160/a2)+(18/b2)=–2
{(96/a2)–(18/b2)=1
Складываем
–64/a2=–1
a2=64
18/b2=(96/a2)–1
b2=36
О т в е т. (x2/64)–(y2/36)=1
в)D: y=1
если каноническое уравнение параболы имеет вид
x2=–2py, то фокус параболы
F(0;–p/2)
D: y=p/2
Значит,
p/2=1
p=2
О т в е т. x2=–4y
Пошаговое объяснение: