Деталь может обрабатываться на любом из имеющихся двух станков. производительность первого станка в 3 раза больше производительности второго. из партии обработанных двумя станками деталей наудачу берут (последовательно с возвратом) три детали. найти вероятность того, что из взятых деталей первым станком обработана одна.
тема: подсчет вероятностей​

Пошаговое объяснение:

1) 12 = 2 * 2 * 3

18 = 2 * 3 * 3

НОК (12; 18) = 2 * 2 * 3 * 3  = 36 - наименьшее общее кратное

2) 14 = 2 * 7

28 = 2 * 2 * 7

НОК (14; 28) = 2 * 2 * 7 = 28 - наименьшее общее кратное

3) 8 = 2 * 2 * 2

9 = 3 * 3

НОК (8; 9) = 8 * 9 = 72 - числа 8 и 9 взаимно простые, потому что не имеют общих делителей, кроме единицы.

1) 24 = 2 * 2 * 2 * 3

42 = 2 * 3 * 7

НОД (24; 42) = 2 * 3 = 6 - наибольший общий делитель

2) 128 = 2 * 2 * 2 * 2 * 2 * 2 * 2

192 = 2 * 2 * 2 * 2 * 2 * 2 * 3

НОД (128; 192) = 2 * 2 * 2 * 2 * 2 * 2 = 64 - наибольший общий делитель

Пошаговое объяснение:

а) разделил на 2 интеграла по разности, под первым e^(pi) - константа, поэтому получится e^(pi) * x = pi* e^(pi) - 0 ( при подстановке)

второй - табличный = sinx + C = 0 в подстановке.

ответ: pi* e^(pi)

б) занесу cosx под дифференциал

cosxdx = d ( sinx + 1)

дальше простой степенной интеграл = 1/3*(1+sinx)^3 + C = 1/3 * (1)^3 - 1/3 * (1)^3 = 0

в) опять под дифференциал

d(4-t^2) = -2*t dt => tdt = -1/2 * d(4-t^2)

дальше простой степенной интеграл = -1/2*2*(4-t)^(1/2) + C = -3^(1/2) + 4^(1/2) = 2 -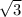

г) под дифференциал:

d(1 + 4x^3) = 12x^2 dx => 6x^2dx = 1/2 d(1+4x^3)

дальше табличный интеграл = 1/2 * ln(1+4x^3) + C = 1/2*ln5 - 1/2*ln1 = 1/2*ln5