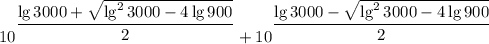ответ: 130
Пошаговое объяснение:
можно прологарифмировать обе части равенства (они строго положительны) по любому основанию (удобно основание 10)
получим два корня: х₁=30; х₂=100
и всегда полезно делать проверку...
Прологарифмируем по основанию 10 обе части уравнения
Пусть , получаем такое уравнение относительно t
Выполним обратную подстановку
Сумма корней
ответ: 130
Пошаговое объяснение:
можно прологарифмировать обе части равенства (они строго положительны) по любому основанию (удобно основание 10)
получим два корня: х₁=30; х₂=100
и всегда полезно делать проверку...
Прологарифмируем по основанию 10 обе части уравнения
Пусть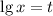
, получаем такое уравнение относительно t
Выполним обратную подстановку
Сумма корней