Найти точку M(x0,y0) условного экстремума функции z(x,y)= 10=2x^2+8xy+8y^2 при ограничении 8x+5y=88. Определить характер экстремума: m=1, если M - точка максимума:; m=-1, если M - точка минимума. Найти число E - экстремальное значение функции. ответ: (x0+y0+E)*m.

Показать ответ

Ответ:

kristinka140320

05.02.2021 03:54

Ну здесь эти уравнения очень тонко намекают на то, какая у нас линия. Смотри.
а) Вспоминаем уравнение эллипса. В нем есть x^2 + y^2

+ какие-то множители и единичка. Смотрим на задание. Тоже x^2 + y^2

! Ну чудесно, теперь можно выполнять алгебраические трюки.
Смотрим еще раз на уравнение. Для удобства можно поменять местами слагаемые: 4x^2-16x+9y^2 - 18y

. Очень похоже на полный квадрат. Прибавляем-вычитаем то, чего не хватает 4x^2-16x+16-16+9y^2 - 18y+9-9 = 0

и сворачиваем (2x - 4)^2-16+(3y - 3)^2 -9 = 0

. После нехитрых преобразований (2x - 4)^2+(3y - 3)^2 = 25

, $\frac{4}{25} (x - 2)^2+ \frac{9}{25} (y - 1)^2 = 1.$ .Вот тебе и эллипс с $a = \frac{25}{4}$ и $b = \frac{25}{9}$ .
б) Смотрим на уравнение. У нас есть y^2

, но нет

. Очень, очень похоже на параболу с каноническим видом y^2 = 2px

. Снова делаем алгебраические трюки, ака преобразования.
y^2-2x-6y-15=0

. Вот и парабола с p = 1.
И тебе, и мне будет дешевле, если ты просто вобьешь свои уравнения в вольфрам и оттуда срисуешь картинки.

0,0(0 оценок)

Ответ:

Ahela007

09.08.2022 16:19

Мы рассматриваем числа в десятичной системе. Это означает, что "цена" разряда - последовательные степени десятки. Например, число из примера можно расписать так:

$\overline{abcd}=a\cdot10^3+b\cdot10^2+c\cdot10^1+d\cdot10^0$

Можно заметить, что все слагаемые в этой сумме, кроме последнего, делятся на 10 (в данном случае второе с конца равно 10c, третье 100b, четвертое 1000a. Но и в общем случае ситуация, очевидно, не меняется).

Остаток от деления натурального числа x на натуральное число y - такое целое число r,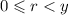 $0\leqslant r$ , что найдётся целое число q, удовлетворяющее равенству 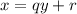x=qy+r . Иначе говоря, (x - r) должно делиться на y.

d - это натуральное число,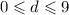 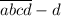$0\leqslant d\leqslant 9$ , $\overline{abcd}-d$ делится на 10, значит, d - остаток от деления исходного числа на 10.

А из того, что

$\overline{\cdots abcd}=\cdots+a\cdot10^3+b\cdot10^2+c\cdot10^1+d=\\=10(\cdots+a\cdot10^2+b\cdot10^1+c\cdot10^0)+d=10\times\overline{\cdots abc}+d$

следует, что после деления на 10 целая часть от деления (q в приведенных выше обозначениях) - это исходное число, но с отброшенной последней цифрой. Для этого числа всё написанное тоже выполняется, поэтому следующий остаток - c, а следующее неполное частное - исходное число без двух последних цифр. Ну и так далее, пока не получится число из одной цифры, она и будет последним остатком, дальше пойдут нули.

Если хочется немного более формального оформления, можете погyглить, что такое принцип математической индукции. По сути, описанное - как раз он, и из него следует, что доказанное утверждение справедливо не только для чисел с не более чем четырьмя цифрами, а вообще для всех натуральных чисел.

0,0(0 оценок)

Популярные вопросы: Математика