Точка М делит сторону AC треугольника АВС в отношении 2: 1, считая от точки А. Найдите вероятность того, что случайно выбранная в треугольнике ABC точка принадлежит треугольнику ВМС.
Вспомним признак делимости на 9: число делится на 9 тогда и только тогда, когда его сумма цифр делится на 9.
Этот признак работает и для равноостаточности при делении на 9. То есть, число и его сумма цифр имеют одинаковый остаток при делении на 9.
Пусть - изначальное число и - сумма цифр числа . Пусть остаток при делении на 9 у числа - r, тогда и у числа остаток при делении на 9 тоже r. Но тогда и у чисел остаток при делении на 9 равен r. Но так как r - чисто от 0 до 9, то это и есть наша оставшаяся в конце цифра.
Тогда нам нужно всего лишь найти остаток при делении на 9 у числа . А он такой же, как у числа , и такой же, как у числа , и такой же, как у числа , а он такой же, как у числа , а это равно 7.
P AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SPAM
SAM
AM
AMP
AMSP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AMSP
ASP
SP
SPM
SPAM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SPAM
SAM
AM
AMP
AMSP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AMSP
ASP
SP
SPM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
Must Waste More Time...
7
Пошаговое объяснение:
Вспомним признак делимости на 9: число делится на 9 тогда и только тогда, когда его сумма цифр делится на 9.
Этот признак работает и для равноостаточности при делении на 9. То есть, число и его сумма цифр имеют одинаковый остаток при делении на 9.
Пусть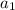
- изначальное число и 
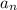- сумма цифр числа 
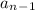. Пусть остаток при делении на 9 у числа 
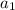- r, тогда и у числа 
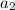остаток при делении на 9 тоже r. Но тогда и у чисел 
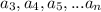остаток при делении на 9 равен r. Но так как r - чисто от 0 до 9, то это и есть наша оставшаяся в конце цифра.
Тогда нам нужно всего лишь найти остаток при делении на 9 у числа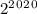
. А он такой же, как у числа 
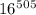, и такой же, как у числа 
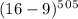, и такой же, как у числа 
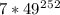, а он такой же, как у числа 
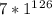, а это равно 7.