1) cosx≥0 - так как под корнем четной степени. sinx≥0, так как иначе Значит, решения могут быть только в I квадранте (включая границы). 2) Очевидно, что x1=2πn и x2=π/2+2πn являются решениями данного уравнения. В первом случае sinx=0, cosx=1, во втором sinx=1, cosx=0. 3) Покажем, что других корней быть не может. Найдем производную функции Так как x - в первом квадранте, то sinx постоянно возрастает, cosx постоянно убывает, значит "первая часть" в производной постоянно убывает от +∞ (справа при стремлении к 0) до 0 (в π/2), а "вторая часть" постоянно возрастает от 0 (в 0) до +∞ при стремлении к π/2. Это значит, что производная положительна до некого x_max на [0;x_max) и отрицательна на (x_max;π/2], принимая одно нулевое значение в x_max на отрезке [0;π/2] Так как на концах отрезка [0;π/2] рассматриваемая функция принимает значения, равные 1, во всех остальных точках отрезка [0;π/2] она принимает значения строго больше 1. Следовательно, других корней исходного уравнения нет.
sinx≥0, так как иначе
Значит, решения могут быть только в I квадранте (включая границы).
2) Очевидно, что x1=2πn и x2=π/2+2πn являются решениями данного уравнения. В первом случае sinx=0, cosx=1, во втором sinx=1, cosx=0.
3) Покажем, что других корней быть не может.
Найдем производную функции
Так как x - в первом квадранте, то sinx постоянно возрастает, cosx постоянно убывает, значит "первая часть" в производной
постоянно убывает от +∞ (справа при стремлении к 0) до 0 (в π/2),
а "вторая часть"
постоянно возрастает от 0 (в 0) до +∞ при стремлении к π/2.
Это значит, что производная положительна до некого x_max на [0;x_max)
и отрицательна на (x_max;π/2], принимая одно нулевое значение в x_max на отрезке [0;π/2]
Так как на концах отрезка [0;π/2] рассматриваемая функция принимает значения, равные 1, во всех остальных точках отрезка [0;π/2] она принимает значения строго больше 1.
Следовательно, других корней исходного уравнения нет.
По условию: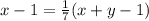 .
.
Получаем первое уравнение:
Ещё по условию: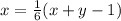 .
.
Второе уравнение:
Левые части обоих уравнений равны, значит, их правые части равны между собой.
Подставим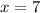 в уравнение
в уравнение 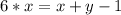 и получим:
и получим:
ответ: 7 красныx;
36 жёлтых;
43 всего шаров в коробке.