Тип: дифференциальное уравнение второго порядка, допускающее понижения порядка.
Пусть , тогда , получаем :
Умножим обе части уравнения на , получаем
Интегрируем обе части уравнения
В правой части уравнения интеграл будем считать путём интегрирования по частям
Выполним обратную замену
ответ: .
Тип: дифференциальное уравнение второго порядка, допускающее понижения порядка.
Пусть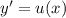 , тогда
, тогда 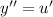 , получаем :
, получаем :
Умножим обе части уравнения на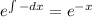 , получаем
, получаем
Интегрируем обе части уравнения
В правой части уравнения интеграл будем считать путём интегрирования по частям
Выполним обратную замену
ответ: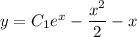 .
.