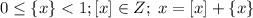с алгеброй Сума перших трьох членів геометричної прогресії 21, а с ума їх квадратів 189. Знайти перший член і знаменник
(ПІДКАЗКА: на презентації одного з відео уроків)
№2 Знайти перший член геометричної прогресії, яка складається з 6 членів, якщо сума трьох її членів з непарними номерами 546, а сума інших трьох 182
№3 Запишіть у вигляді звичайного дробу число 5,1(6)
(ПІДКАЗКА: підручник стр 360, приклад 1
№4 Сума перших n членів деякій послідовності знаходиться за формулою S_n=5^n/(2^n+3^n ) . Чи є ця послідовність геометричною прогресією?
№5 (x_n) нескінченна спадна геометрична прогресія, у якої x_1=3,q=1/3 . знайти суму її членів з непарними номерами
№6 Сума членів нескінченної спадної геометричної прогресії дорівнює 3, а сума її кубів 108/13 Записати три перших члена цієї прогресії
(ПІДКАЗКА: скористайтеся формулою b_n=b_1∙q^(n-1) 2) розв’яжіть систему
№7 С ть рівняння функції у=х^4+х^4/(1+х^4 )+х^4/(1+х^4 )^2 + Знайти її значення при х=3
(ПІДКАЗКА: 1) з’ясуйте чи буде права частина рівняння нескінченою геометр прогресією 2) якщо так, то можна знайти її суму
По определению,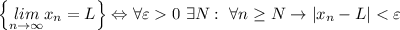
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение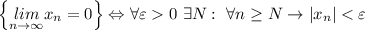
2)
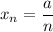
А значит, если взять![N=\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/0d89e.png)
(*), 
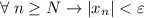. И правда: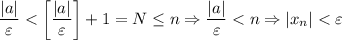 
(*) Очевидно, что для любого допустимого значения
выражение ![\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/ae843.png)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4)
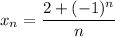
А значит, если взять![N=\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/a4ca4.png)
(**), 
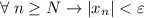. И правда: ![\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|](/tpl/images/3820/0626/49458.png)
(**) Очевидно, что для любого допустимого значения
выражение ![\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/698f8.png)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда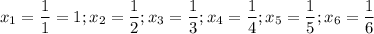
4)
___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x.