Учень навмання витягнув один з 25 екзаменаційних білетів, пронумерованих
послідовно від 1 до 25. Знайти ймовірність того, що номер узятого білета:
1) ділиться на 3; 2) ділиться на 4.

На числовой прямой:

t и -t

Числа имеют противоположные знаки и |t| = |-t|. Точки симметричны относительно нуля.

t и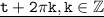

k=0 ⇒ точки совпадают.

k<0 ⇒ t правее t+2πk на 2πk

k>0 ⇒ t левее t+2πk на 2πk.

t и t+π

t левее t+π на π.

t+π и t-π

t+π правее t-π на 2π.

На числовой окружности:

t и -t

Точки симметричны относительно оси абсцисс (Ox).

t и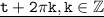

Точки совпадают т.к. 2π это целый круг.

t и t+π

Точки симметричны относительно начала координат т.к. π это половина круга.

t+π и t-π

Точки совпадают т.к. они различаются на 2π, а это целый круг.

ответ:  x ∈ (-∞; 0) ∪ (3; +∞) .  

Сначала решим первое неравенство (методом интервалов). В первой скобке получается нуль, если подставить 3. Во второй - если подставить -6. Отмечаем эти числа на числовой оси и ставим нужные знаки (рисунок 1, в приложении). Знак неравенства строгий, поэтому все точки выколотые.

Теперь решаем второе неравенство. Нуль в числителе получается, если подставить -6 (точка закрашенная, знак неравенства нестрогий). А в знаменателе - если подставить 0 (точка выколотая, по всем правилам арифметики на нуль делить нельзя). Теперь ставим нужные знаки (рисунок 2, в приложении).

Теперь объединяем все решения двух неравенств (рисунок три, приложение) и записываем окончательный ответ:

x ∈ (-∞; 0) ∪ (3; +∞) .