Вадим и Толик получили одинаковый комплект задач на кружке. Известно, что оба мальчика каждую задачу приходили сдавать 2 , 3 или 5 раз. У преподавателя отмечено, что Вадим приходил сдавать задачи 93 раз(-а), а Толик — 41 раз(-а). Могло ли такое быть? Если да, сколько задач было на кружке? ( начисляются только за полностью верный ответ!)
4х²-2х+3=0
D=(-2)²-4×4×3=4-48=-44 D<0, уравнение не имеет корней
----------------------------------------------------------------------------
5х²+26х=24
5х²+26х-24=0
D=26²-4×5×(-24)=676+480=1156 D>0
х₁=
х₂=
х₁=0,8
х₂=-6
-------------------------------------------------------------------------
3х²-5х=0
D=5²-4×3×0=25-0=25 D>0
х₁=
х₂=
х₁=1,667
х₂=0
--------------------------------------------------------------------
6-2х²=0
-2х²+6=0
D=0²-4×(-2)×6=0+48=48 D>0
х₁=
х₂=
х₁=-1,732
х₂=1,732
------------------------------------------------------------------
t²=35-2t
t²+2t-35=0
D=2²-4×1×(-35)=4+140=144
t₁=
t₂=
t₁=5
t₂=-7
Заданные в условии числа - это угловые меры в радианах.
360° = 2π ≈ 6,28 радиан полный оборот.
180° = π ≈ 3,14 радиан - развёрнутый угол.
90° = π/2 ≈ 1,57 радиан - прямой угол.
На числовой окружности отсчёт углов начинается от положительного направления оси ОХ : положительные угловые меры против часовой стрелки, отрицательные - по часовой стрелке. Чтобы построить точку на окружности, можно перевести радианы в градусы и воспользоваться транспортиром.
а)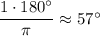
0° < 57° < 90° ⇒ 1 в первой четверти
б)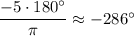
; -286° + 360° = 74°
0° < 74° < 90° ⇒ (-5) в первой четверти
в)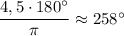
180° < 258° < 270° ⇒ 4,5 в третьей четверти
г)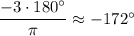
-180° < -172° < -90° ⇒ (-3) в третьей четверти