Пусть «» кг раствора было изначально ⇒ доля соли в этом растворе ⇒ кг раствора стало после добавления соли ⇒ доля соли в конечном растворе. Т.к. доля соли после добавления увеличилась на 15% (), получим:
Домножим обе части уравнения на и , получим:
Перенесём правую часть уравнения в левую, получим:
Квадратное уравнение вида можно решить с дискриминанта .
⇒ корней будет два.
По условию концентрация соли в первоначальном растворе была меньше 20% ⇒ (массовая доля соли в первоначальном растворе) должна быть .
30 кг
Объяснение:
Пусть « » кг раствора было изначально ⇒
» кг раствора было изначально ⇒ 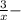 доля соли в этом растворе ⇒
доля соли в этом растворе ⇒ 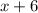 кг раствора стало после добавления соли ⇒
кг раствора стало после добавления соли ⇒ 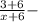 доля соли в конечном растворе. Т.к. доля соли после добавления увеличилась на 15% (
доля соли в конечном растворе. Т.к. доля соли после добавления увеличилась на 15% (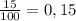 ), получим:
), получим:
Домножим обе части уравнения на и
и 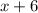 , получим:
, получим:
Перенесём правую часть уравнения в левую, получим:
Квадратное уравнение вида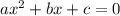 можно решить с дискриминанта
можно решить с дискриминанта 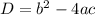 .
.
По условию концентрация соли в первоначальном растворе была меньше 20% ⇒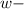 (массовая доля соли в первоначальном растворе) должна быть
(массовая доля соли в первоначальном растворе) должна быть  .
.
Значит, первоначальная масса раствора была 30 кг.
Объяснение:
Упростим выражение (х - 5)^2 - х(10 + х) и найдем его значение при x = - 1/20.
Откроем скобки в выражении. Первую скобку открыть формула сокращенного умножения — квадрат разности (a - b)^2 = a^2 - 2ab + b^2;
Вторую скобку мы откроем при дистрибутивного закона умножения и правила открытия скобок перед которыми стоит знак минус.
(x - 5)^2 - x(10 + x) = x^2 - 10x + 25 - 10x - x^2 = - 10x - 10x + 25 = - 20x + 25;
Найдем значение выражения при x = - 1/20:
- 20x + 25 = - 20 * (- 1/20) + 25 = 1 + 25 = 26.